Analog style video synthesis by computer animation

Some experimental video artists began making video by directly synthesizing images without external input in the 1960's. Colours are built up additively by mixing red, green and blue. Images were constructed from patterns of spatial frequencies. There were studios with expensive gear for special effects that could be hired for TV shows or commercials. Pioneering artists like Nam June Paik built their own video synthesizers. The Experimental Television Center has been around from 1971 and numerous artists have worked there on their residency program.

I don't know too much about the equipment and techniques used. A few things can be deduced from the visual appearance of the videos. Today there is no lack of analog video synthesis modules that perform all kinds of processing and signal generation.

In my own work with computer animation so far I have made videos with moving, and occasionally metamorphosing objects. Recently I have started experimenting with simulations of analog video synthesis. The approach couldn't be more different.

In some respect video synthesis is simpler than object-based animation. You don't have to build objects with moving parts and do a lot of geometrical calculations. Each colour channel can be treated independently. You don't need a storyboard with a plot, it is better to adopt an open-minded experimenter's attitude, to try and fail, try again and maybe succeed.

Fourier transforms for images

Spatial frequency is the key concept. Horizontal and vertical patterns of alternating stripes are easy to make. Low frequencies correspond to wide stripes, high frequencies result in narrow stripes, until the waveform alternates at the pixel resolution. As in additive synthesis of audio signals one has to watch out for aliasing. Waveforms can be composed as sums of sinusoids with given amplitudes and phases.

Rotations and stripes at various angles is the next step. One has to think in terms of vectors, where wavefronts in some oblique direction are composed of sums of horizontal and vertical components (or generally any pair of basis vectors). The complete image may be synthesised by the inverse Fourier transform. Now the 2D Fourier transform was not something I had ever used, despite years of familiarity with its one-dimensional version, so I had to look up its definition.

In the one-dimensional continuous case time and frequency are defined over the real numbers. The complex frequency may be split into a sine and cosine term for convenience, or one can use the cosine plus phase form, according to taste.

1D:

x(t) = ∫ X(ω)exp(-iωt)dω

In two dimensions frequency has vertical and horizontal components, u and v, which are both complex valued.

2D:

Forward

F(u,v) = ∬f(x,y)exp(-i2π(ux + vy))dxdy

Inverse

f(x,y) = ∬ F(u,v)exp(i2π(ux + vy))dudv

The 2D Fourier transform has some useful applications in image processing, but here the idea is rather to define a spectrum ad hoc and synthesise images from it. First of all, it turns out the Fourier transform is a complex and rather slow operation unless performed using the FFT, and the 2D transform is even slower. Secondly, the spatial frequency representation is not very intuitive. Sharp edges are produced by sums of frequency components that have to have the exact right spatial angles and amplitudes. I tried a few variations of spectral synthesis, not by specifying the full Fourier spectrum but by sparse representations where just a handful of frequency components were given. The images were typically grainy textures of blobs more or less evenly dispersed across the image.

Additive synthesis from Fourier spectrum (jpg, ~ 177 kB)

🖼️

Wavetable synthesis

A more efficient synthesis method is to calculate periodic waveforms and store them in tables. Wavetable synthesis is a popular synthesis technique for sound, where the requirements are perhaps more demanding in some ways than in video synthesis. I had a library of waveforms ready to try out and so I did. For audio applications the spectrum, and in particular the amplitudes of the partials, is of primordial importance, but in vision we perceive in terms of waveforms. There are interesting cross-modal correspondances: Higher frequencies of audio or spatial alternations as perceived by touch or vision appear smaller, finer, sharper, and lower frequencies as duller, softer, and bigger.

Anyway, some waveforms that are interesting to use for audio are less suitable for video, and possibly vice versa. The Gibbs phenomenon of ringing around sharp edges may be more acceptable in audio, whereras in video it may look as poor compression. Visual artefacts of aliasing can be seen in naïve line drawing algorithms when the lines don't align with the rows of pixels. It can be exploited as a feature in retro-style imagery, in other contexts it doesn't look pretty.

Geometry

Rectangular coordinates have their limitations. Although any image can be synthesized from a 2D Fourier spectrum it can take a lot of components to approach any semblance of similarity with the target. If you fancy drawing anything like circles or spirals polar coordinates is a practical necessity. Various distance functions can be handy too, not just Euclidian, but also Manhattan metrics and what have you.

Example with masking (jpg)

🖼️

Another example with masking (jpg)

🖼️

Masking can be used to display different colours or patterns in specific shapes. Some linear algebra for straight line equations and a bit of modulo arithmetic and logical operators can be used for making checkerboards and other simple patterns.

Feedback and nonlinear functions

Similar to audio synthesis, complex forms can be easily synthesized by nonlinear techniques such as frequency modulation. Add to that a bit of feedback and really complex images begin to appear.

One interesting form of feedback is to take adjacent, previously computed pixel values and feed them into the function that calculates the current pixel. The colour channels can feed into each other or act separately.

For even more intriguing results one can apply feedback from the previous image frame to the current frame. This is roughly what happens with analog video feedback when you turn the camera towards the monitor that shows an image of itself in an image of itself ... and so on. Analog video feedback of course is extremely complicated to model because of all kinds of geometric and optical distortions and convolutions that twist the image. Jim Crutchfield once wrote a fascinating paper about the phenomenon.

Digital video feedback, let's say just from the same pixel at the previous frame, is a bit different from its analog counterpart. If you make the feedback some nonlinear function of the previous pixel it becomes an iterated map, and as such we know what classes of dynamics there are: chaos, which might be fun, periodic or perhaps quasi-periodic oscillations, or boring steady-state solutions, as well as shortlived initial transients to any of these states. In any iterated map its parameter space may have regions of period two solutions, smaller regions of period four, any other periods, chaos, and fixed points. Solutions of short periodicity imply that the pixel will flicker rapidly between two or a few values. Unless intended such flickering can be annoying (well, it can be even if intentional).

In some experiments I did with such iterated maps there was not just lots of flickering, the image tended to organise into patterns of high spatial frequency too, with alterating intensities at every line of pixels. For small image sizes the details may still be discernible, but with larger images displayed with higher pixel density the effect tends towards an indistinct blur.

Iterated map causing high spatial frequency (jpg)

🖼️

Currently I'm trying to make thumbnail images of the previous frame that will be used for feedback after being rescaled to original size. This way there is some spatial averaging which should remove some high frequency content.

Video delays involving feedback from past frames at longer time delays have been used to great effect. Digital implementations are not trivial, at the very least one has to allocate a lot of memory to store each frame between the current one and the delayed one.

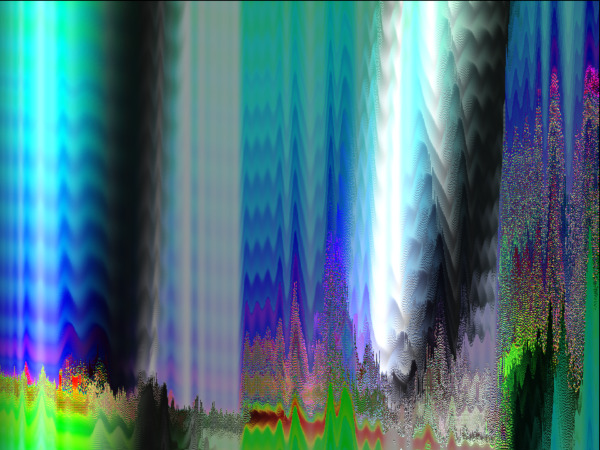
Colour space

Video synthesis is all about saturated, glowing, psychedelic colours. It just seems to be a side effect of how images are generated. A few pixels here and there may be some shade of gray, but colour perception is not about a few isolated pixels, it is about broader surfaces.

It isn't difficult to work with specific colour schemes though. Instead of specifying r,g,b triplets one can turn to hue, saturation, and value. Then the grays enter the picture with authority and find their proper place alongside the saturated colours.

HSV-encoded still (jpg)

🖼️